Ötletek egy gazdaságos, mégis varázslatos karácsonyhoz Ahogy közeledik a karácsony, sokan keresnek módokat arra, hogyan ünnepelhetnének anélkül, hogy túllépnék a költségvetésüket. Takarékos karácsony nemcsak pénztárcabarát, hanem kreatív és különleges él
Érdemes elgondolkodnunk az olyan háromszögeken is, amelyek nem a megszokott pozíciójukban helyezkednek el, például amikor a szárukon fekszenek. Emellett fontos megjegyezni, hogy a háromszög belső szögeinek összege mindig 180 fokot tesz ki, ami éppen egy egyenesszögnek felel meg.
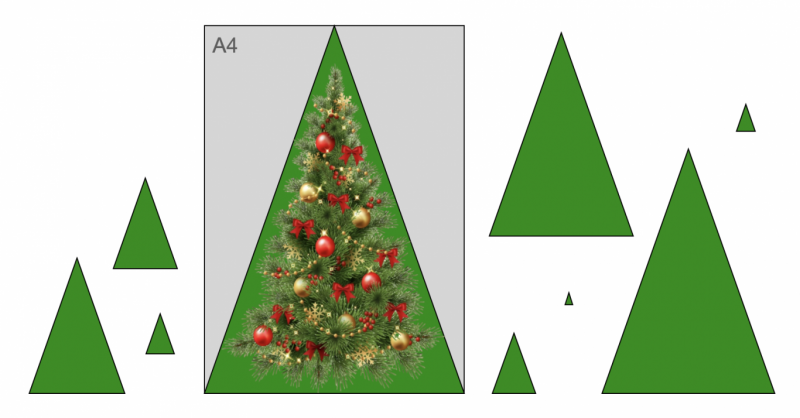
Egy lehetséges ötlet a következő darabolás.
Mielőtt azonban ezt elfogadjuk, három dolgot ellenőrizni kell: hogy tényleg hasonlóak-e a háromszögek, hogy vágásonként egy háromszög leesik-e, illetve hogy különböző méretűek-e.
Az 1-es sorszámmal jelölt háromszöget levághatjuk úgy, hogy egyenlő szárú legyen, és egyik szöge (jobb alsó) az eredetivel megegyezik, így a háromszög is hasonló lesz az eredetihez. Hasonlóan a 2-es sorszámú háromszögnek is van az eredetivel megegyező szöge (a szárszöge), és ha az alapok párhuzamosak egymással, akkor ezek is hasonlóak lesznek. A 3-as sorszámú háromszögnek pedig azért lesz a szárszöge (a két szár közötti szöge) megfelelő, mert az 1-es, 2-es és 3-as háromszög közös csúcsában találkozó szögek épp egy egyenesszöget adnak ki, ami egyben a háromszög szögeinek összege. Innentől kezdve teljesen hasonló módon adódik, hogy a 4-es szárszöge is épp megfelelő, mert a 2-es, 3-as és 4-es háromszög közös csúcsában találkozó szögek összege is 180 fok, és így tovább. A hasonlóság tehát belátható, ha pedig az ábrán jelölt sorszámok szerinti sorrendben haladunk, akkor az is látható, hogy minden egyes vágással keletkezik egy új háromszög, amit a későbbiekben már nem kell tovább vágunk, tehát fel tudjuk azonnal ragasztani.
Amit még meg kell vizsgálnunk, az a háromszögek méretének eltérése. A 3-as sorszámú háromszög esetében ez már egyértelmű, hiszen minden levágott háromszög szára az előző háromszög alapjára épül, így a következő levágott háromszög mérete ugyanazzal a kicsinyítési faktorral alakul. Az igazi kérdés az, vajon az 1-es és 2-es sorszámú háromszögek méretei is eltérnek-e egymástól. Első pillantásra úgy tűnik, hogy valóban így van, amit egy A4-es lap segítségével is ellenőrizhetünk, ahogyan azt a méretarányos ábrázolás is mutatja. Mivel azonban fontos a pontos megerősítés, ezt a számítást a kedves olvasóra bízom.





